Chapter 18 Logistic Regression: Introduction

So far, we have always assumed that our outcome variable was continuous. But when the outcome variable is binary (almost always coded as 0/1), we need to change our model.

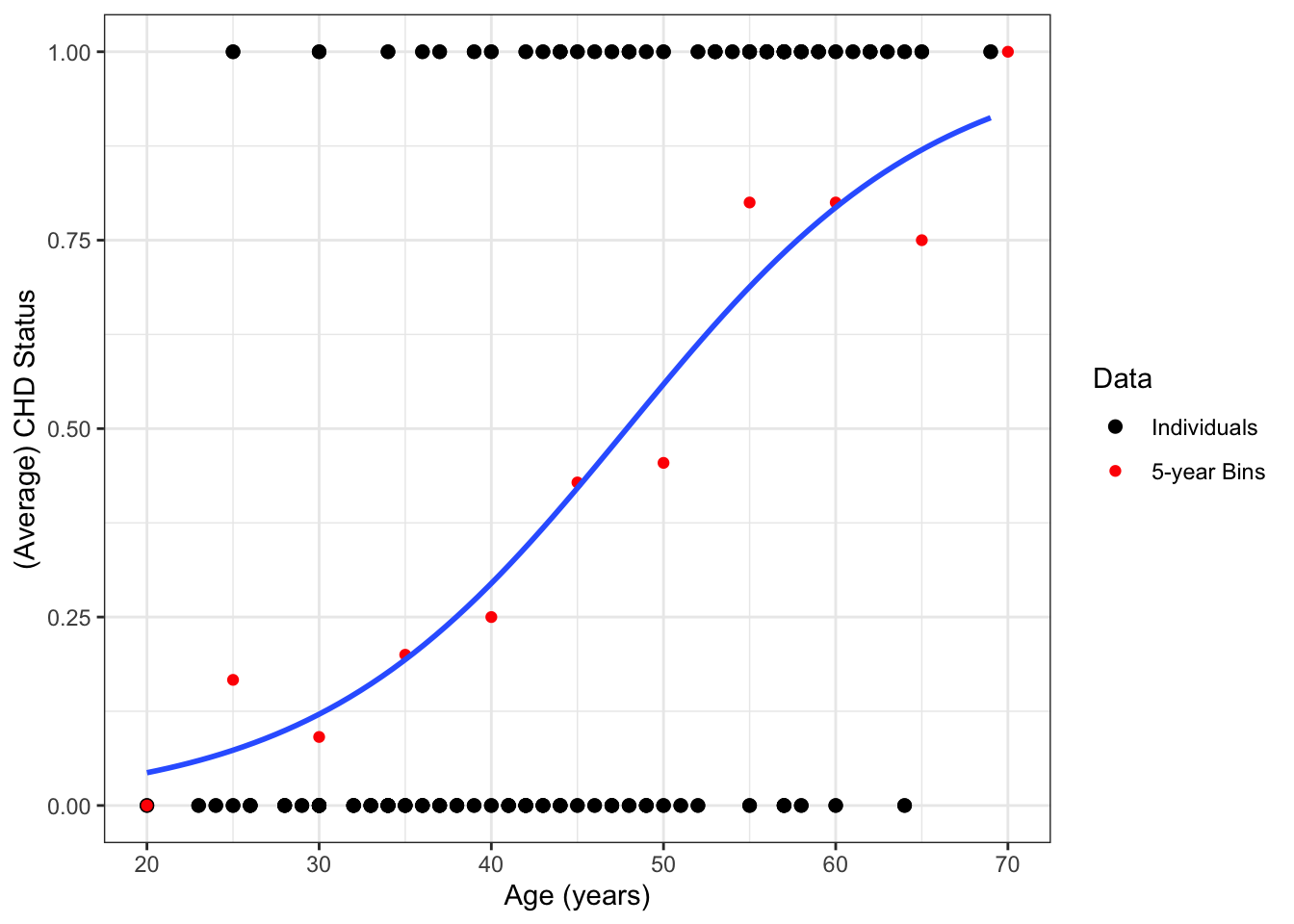
Example 18.1 In a sample of 100 U.S. adults, we have data on their coronary heart disease (CHD) status and age (in years). These are plotted in Figure 18.1.

Figure 18.1: Plot of raw CHD data. Note that some points are overlapping here.

Table 18.1: Proportion of CHD cases in five-year age bands.

Age Group	Proportion CHD
[17.5,22.5]	0.000
(22.5,27.5]	0.167
(27.5,32.5]	0.091
(32.5,37.5]	0.200
(37.5,42.5]	0.250
(42.5,47.5]	0.429
(47.5,52.5]	0.455
(52.5,57.5]	0.800
(57.5,62.5]	0.800
(62.5,67.5]	0.750
(67.5,72.5]	1.000

How can we model this data?

• For an individual, we observe CHD=1$CHD=1$ or CHD=0$CHD=0$.
• Let p(x)$p\left(x\right)$ denote the probability that CHD=1$CHD=1$ for someone of age x$x$:

p(x)=P(CHD=1|Age=x)$$p\left(x\right)=P(CHD=1|Age=x)$$

What about p(x)=β0+β1x$p\left(x\right)={\beta }_0+{\beta }_{1}x$?

Figure 18.2: A simple linear regression line fit to the CHD data. Red dots show the average rates for five-year age bins.

The regression line in Figure 18.2 extends beyond the range of the data, giving nonsensical values below 25 years of age and above 70 years of age.

In settings like Example 18.1, it is no longer appropriate to fit a straight line through the data. Instead, we need a model that accommodate the limited range of outcome points (between 0 and 1) while still allowing for fitted values to differ by age (the predictor variable).

The key to doing this is the logistic function.

18.1 Logistic and Logit Functions

18.1.1 Logistic Function

The logistic function is given by the equation f(η)=exp(η)1+exp(η)=11+exp(−η)$$\begin{array}{}f\left(\eta \right)=\frac{\exp \left(\eta \right)}{1+\exp \left(\eta \right)}=\frac{1}{1+\exp (-\eta )}& \text{(18.1)}\end{array}$$ and is plotted in Figure 18.3. Key features of the logistic function are:

• As η→∞, f(η)→1
• As η→−∞, f(η)→0
• f(0)=1/2

Figure 18.3: The logistic function.

While Figure 18.3 shows the logistic function in terms of η, it is common to write η as a function of x. Figure 18.4 shows this for several different relationships of the form η=β0+β1x. In that figure, we can see how the logistic function can be shifted and scaled depending upon the values of β0 and β1. This is analogous to modifying the equation for a line using its intercept and slope.

Figure 18.4: The logistic function for different settings of eta.

18.1.2 Logistic Regression

Logistic regression models the probability of an outcome using the logistic function:

P(Yi=1|Xi=x)=p(x)=11+exp(−[β0+β1x])

Why use the logistic function?

• Inputs any value (−∞,∞)
• Outputs a value between 0 and 1
• Provides smooth link between continuous predictor (η=β0+β1x) and a probability P(Y=1).

Example 18.2 In the CHD data from Example 18.1, we can fit the equation: P(CHD=1|Age=x)=11+exp(−[−5.31+0.11x])

The logistic regression equation (18.2) implies a linear model for the log odds (= logit) of Y=1:

logit(p(x))=logp(x)1−p(x)=β0+β1x

Mathematically, this connection can be derived by solving the logistic function (18.1) for η: p=11+exp(−η)p=exp(η)1+exp(η)p(1+exp(η))=exp(η)p+pexp(η))=exp(η)p=exp(η)−pexp(η)p=(1−p)exp(η)p1−p=exp(η)log(p1−p)=η

Note similarity between (18.3) and the equation for simple linear regression: E[Y]=μ=β0+β1x. In both cases, there is a single “intercept” and “slope”, although those parameters have a different effect in the two models.

18.1.3 Odds

The odds of an event happening is the probability that it happens divided by the probability that it does not happen

Odds=p1−p

• Odds are always positive
• Higher odds means higher probability of success; lower odds means lower probability of success
• Odds are most commonly used in logistic regression and in sports betting

Example 18.3 If probability of winning a game is 0.67, the odds of winning are 0.671−0.67=0.670.33=2

18.2 Logistic Regression in R

18.2.1 Fitting Logistic Regression in R

In logistic regression, parameters (β’s) are estimated via maximum likelihood. The details of this procedure are covered in Section 19.

Obtaining estimates in R is similar to simple linear regression, except we use glm instead of lm:

chd_glm <- glm(chd~age, data=chdage, family=binomial)

• First argument is a formula: y ~ x1 + x2 + ...
• The data argument is optional, but highly recommended. data accepts a data frame and the function looks for the variable names in the formula as columns of this data frame.
• Setting family=binomial indicates that we are fitting a logistic regression model (as opposed to other GLM).
• summary() and tidy() provide information similar to linear regression.

chd_glm

## 
## Call:  glm(formula = chd ~ age, family = binomial, data = chdage)
## 
## Coefficients:
## (Intercept)          age  
##     -5.3095       0.1109  
## 
## Degrees of Freedom: 99 Total (i.e. Null);  98 Residual
## Null Deviance:       136.7 
## Residual Deviance: 107.4     AIC: 111.4

summary(chd_glm)

## 
## Call:
## glm(formula = chd ~ age, family = binomial, data = chdage)
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -5.30945    1.13365  -4.683 2.82e-06 ***
## age          0.11092    0.02406   4.610 4.02e-06 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 136.66  on 99  degrees of freedom
## Residual deviance: 107.35  on 98  degrees of freedom
## AIC: 111.35
## 
## Number of Fisher Scoring iterations: 4

tidy(chd_glm)

## # A tibble: 2 × 5
##   term        estimate std.error statistic    p.value
##   <chr>          <dbl>     <dbl>     <dbl>      <dbl>
## 1 (Intercept)   -5.31     1.13       -4.68 0.00000282
## 2 age            0.111    0.0241      4.61 0.00000402

18.3 Risk Ratios and Odds Ratios

18.3.1 Calculating Quantities in Logistic Regression

The fitted logistic regression model is:

logit(ˆp(x))=logˆp(x)1−ˆp(x)=ˆβ0+ˆβ1x

Or, equivalently:

ˆp(x)=11+exp(−[ˆβ0+ˆβ1x])

Using this model, we can calculate the estimated

• The probability ˆp(x) of success. In some contexts (e.g., medicine), this is called the risk.
• risk ratio ˆp(x1)ˆp(x2). This is the ratio of probabilities of success for two different values of the predictor variable.
• The **odds(()) ˆp(x)1−ˆp(x)
• The odds ratio ˆp(x1)1−ˆp(x1)/ˆp(x2)1−ˆp(x2)

18.3.2 Calculating Risk of CHD

Example 18.4 Using the model from Example 18.2, what is the risk of CHD for a 65-year-old person? How does this compare to the risk of CHD for a 64-year-old person?

We estimate p(x) by plugging in our estimates of β0 and β1. ˆp(65)=11+exp(−[ˆβ0+ˆβ1(65)])=11+exp(−[−5.309+0.111(65)])=0.870 “We estimate that the probability of CHD for a 65 year-old person (from this population) is 0.870”

For 64-year-olds, the probablity of CHD is: ˆp(64)=11+exp(−[−5.31+0.11(64)])=0.857 Thus, the risk ratio (RR) for CHD comparing 65- to 64-year-olds is: RR=0.8700.857=1.02 “We estimate that the risk of CHD for a 65 year-old person is 2% greater than that for a 64 year-old person in this population.”

Example 18.5 We can calculate the risk and risk ratio of CHD for other ages:

x	ˆp(x)
65	0.870
64	0.857
51	0.586
50	0.559
31	0.133
30	0.121

Age Comparison	Risk Ratio (RR)
65 v 64	0.870/0.857 = 1.015
51 v 50	0.586/0.559 = 1.049
31 v 30	0.133/0.121 = 1.102

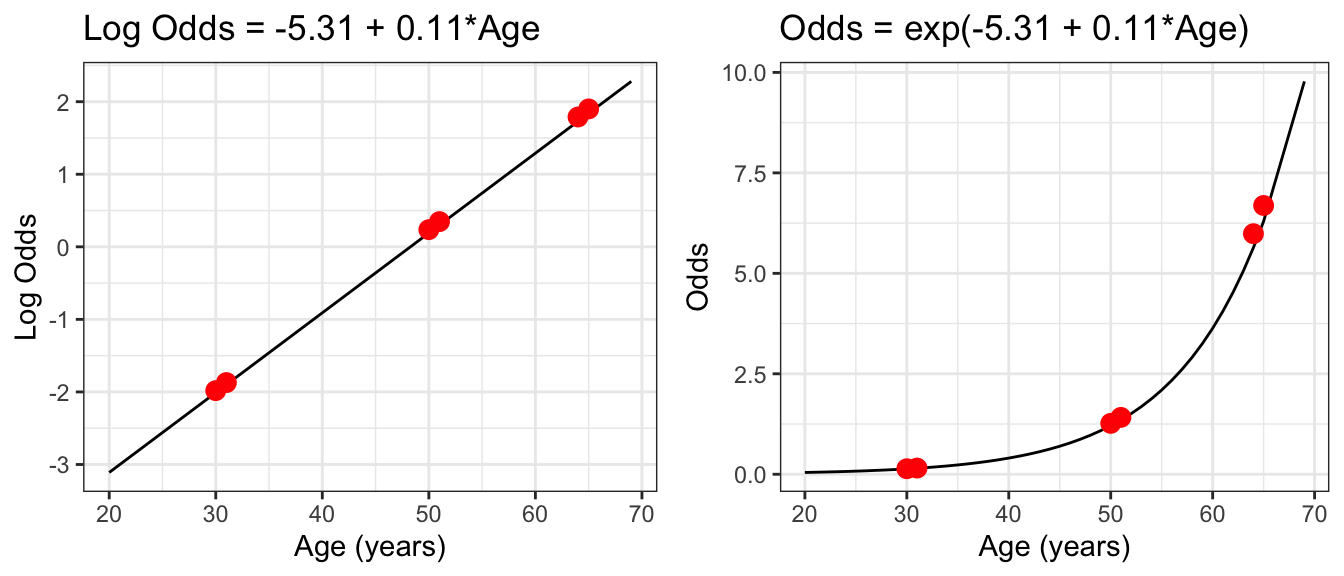
An important result from these tables is that the RRs are not constant! This is because the estimated probabilities are points along this (non-linear!) curve:

## `geom_smooth()` using formula = 'y ~ x'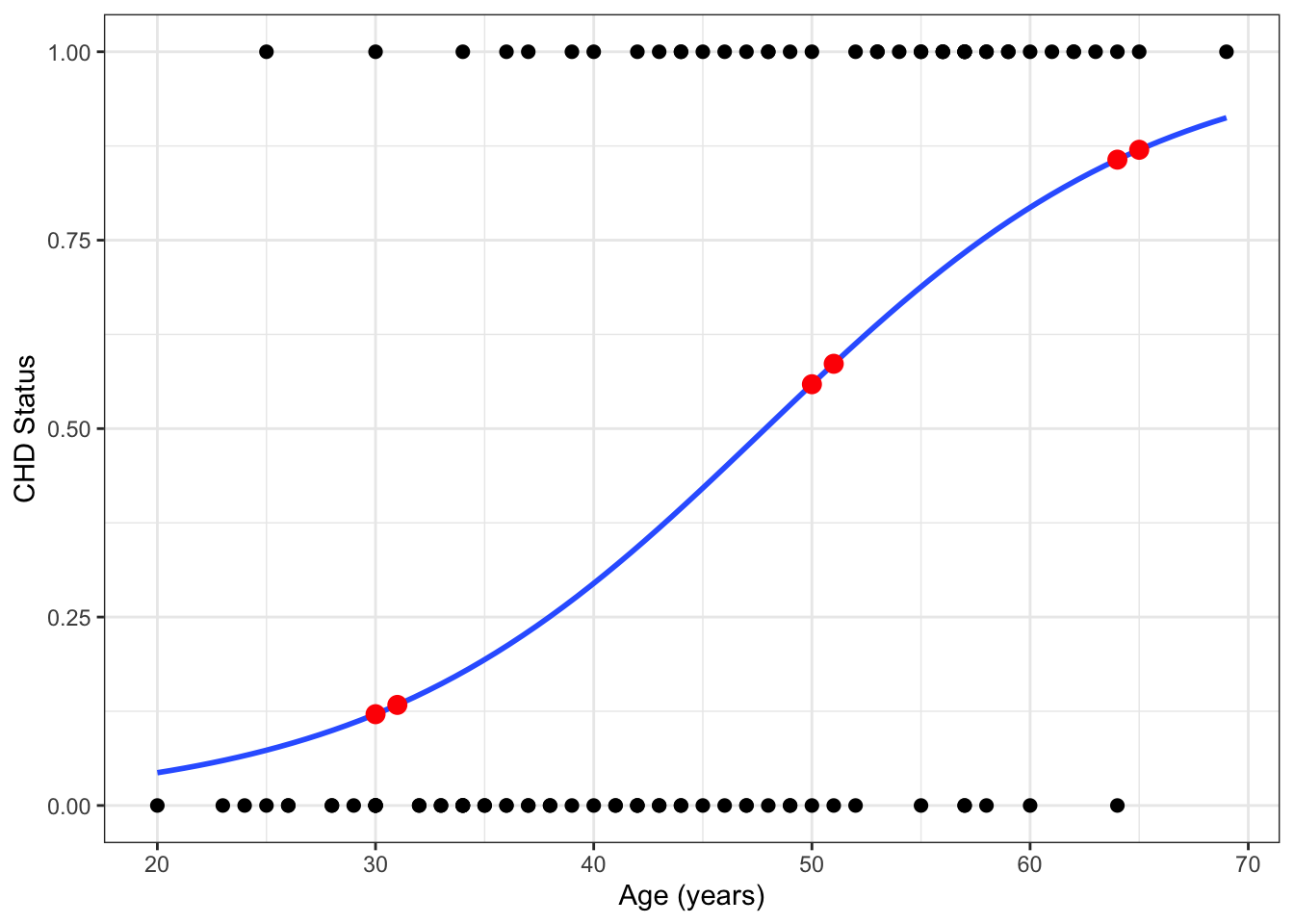

18.3.3 Calculating the Odds

In addition to estimated risk (ˆp), we can calculate the odds that Y=1: Odds of CHD for age x=odds(x)=p(x)1−p(x)=exp(logit(p(x)))=exp(β0+β1x)

Example 18.6 What are the odds of CHD comparing 65 to 64-year-olds?

Plug in our parameter estimates: ^odds(65)=exp(ˆβ0+ˆβ1(65))=exp(−5.309+0.111∗65)=exp(1.90)=6.69 “We estimate that the odds of CHD for a 65 year-old person (from this population) to be 6.69” Note that 0.8701−0.870=6.69 and 6.691+6.69=0.870. What about for 64 year-olds? ^Odds(64)=exp(−5.309+0.111∗64)=exp(1.790)=5.986 So we have:

x	^logOdds(x)	^Odds(x)	ˆp(x)
65	1.900	6.689	0.870
64	1.790	5.986	0.857

The odds ratio for CHD comparing 65- to 64-year-olds is: 6.6895.986=1.117

We can do this for other ages:

x	^logOdds(x)	^Odds(x)	ˆp(x)
65	1.900	6.689	0.870
64	1.789	5.986	0.857
51	0.347	1.416	0.586
50	0.237	1.267	0.559
31	-1.871	0.154	0.133
30	-1.982	0.138	0.121

Odds ratios for CHD are:

Age Comparison	Odds Ratio (OR)
65 v 64	6.689/5.986 = 1.117
51 v 50	1.416/1.267 = 1.117
31 v 30	0.154/0.138 = 1.117

The ORs are constant!

The reason the ORs are constant are because the log-odds regression line is a straight line!

18.4 Interpreting β1 and β0

18.4.1 Interpreting β1

When comparing individuals who differ in age by 1 year,

• additive difference in log-odds is constant
• multiplicative difference in odds (i.e. odds ratio) is constant
• additive and multiplicative differences in risk depend on the specific ages

The logistic model is a linear model for the log-odds: log(p(x)1−p(x))=β0+β1x

Differences of one-unit in x correspond to a β1 difference in log-odds.

log(odds(x+1))−log(odds(x))=log(p(x+1)1−p(x+1))−log(p(x)1−p(x))=[β0+β1(x+1)]−[β0+β1x]=β0+β1x+β1−β0−β1x=β1

Additive differences in log-odds are multiplicative differences in odds:

log(odds(x+1))−log(odds(x))=β1exp[log(odds(x+1))−log(odds(x))]=exp(β1)exp[log(odds(x+1))]exp[log(odds(x))]=exp(β1)odds(x+1)odds(x)=exp(β1)

18.4.2 Interpreting β1: CHD Example

Odds ratios for CHD are:

Age Comparison	Odds Ratio (OR)
65 v 64	6.689/5.986 = 1.117
51 v 50	1.416/1.267 = 1.117
31 v 30	0.154/0.138 = 1.117

ˆβ1=0.11⇒exp(0.11)=1.117

In this population, a difference of one-year in age is associated, on average, with 11.7% higher odds of CHD.

18.4.3 Interpreting β0

The logistic model is a linear model for the log-odds: log(p(x)1−p(x))=β0+β1x

What is β0?

β0=log(p(0)1−p(0))

• The “intercept” for the log-odds
• The log-odds when x=0.
• In most cases, this is of little scientific interest
• In some cases, this has no scientific meaning

18.4.4 Calculating Odds Ratios and Probabilities in R

• As with linear regression, avoiding rounding in intermediate steps when computing quantities
• Instead, use R functions that carry forward full precision

The tedious approach:

coef(chd_glm)

## (Intercept)         age 
##  -5.3094534   0.1109211

1/(1 + exp(-(coef(chd_glm)[1] + coef(chd_glm)[2]*64)))

## (Intercept) 
##   0.8568659

The recommended approach: use predict()

• Set type="link" to compute estimated log-odds
• Set type="response" to compute estimated probabilities

predict(chd_glm, newdata=data.frame(age=64),
        type="link")

##      1 
## 1.7895

predict(chd_glm, newdata=data.frame(age=64),
        type="response")

##         1 
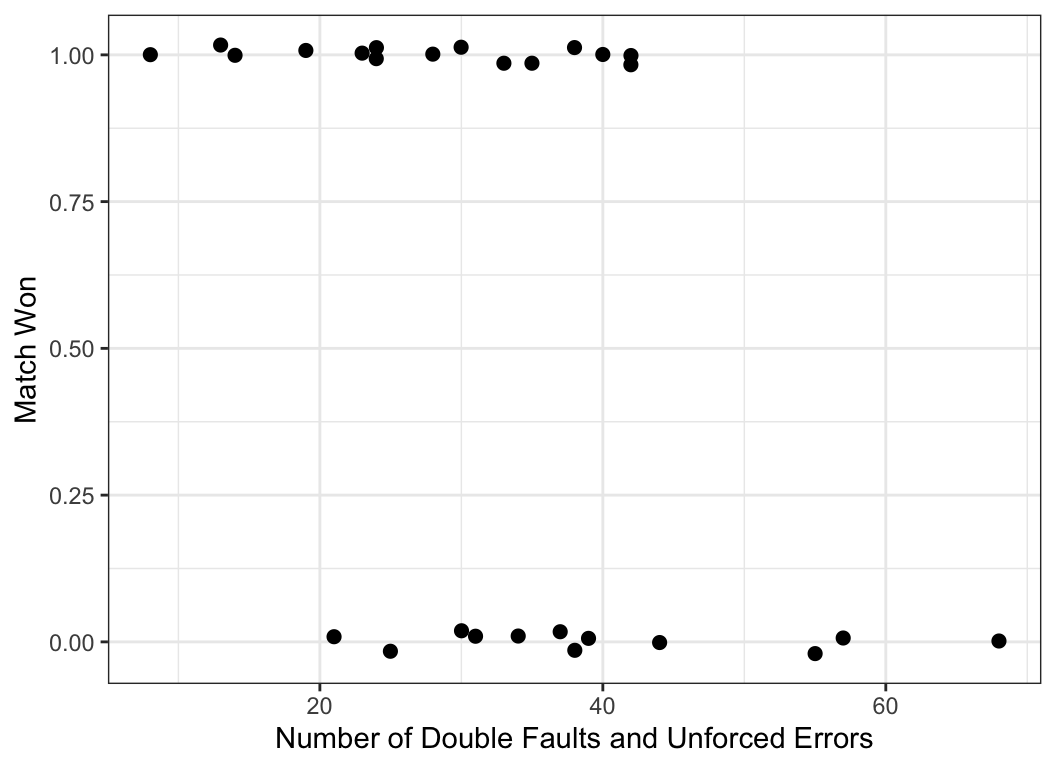
## 0.8568659

Example 18.7 Data are available on the first round of the 2013 Women’s U.S. Tennis Open. Let’s model the probability of the player winning (variable won) as a function of the number of unforced errors and double faults she made (variable fault_err).

open_mod1 <- glm(won~fault_err, 
                 data=usopen,
                 family=binomial)

summary(open_mod1)

## 
## Call:
## glm(formula = won ~ fault_err, family = binomial, data = usopen)
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)  
## (Intercept)  3.23139    1.50329   2.150   0.0316 *
## fault_err   -0.09036    0.04322  -2.091   0.0366 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 37.096  on 26  degrees of freedom
## Residual deviance: 30.640  on 25  degrees of freedom
## AIC: 34.64
## 
## Number of Fisher Scoring iterations: 4

tidy(open_mod1, conf.int=TRUE)

## # A tibble: 2 × 7
##   term        estimate std.error statistic p.value conf.low conf.high
##   <chr>          <dbl>     <dbl>     <dbl>   <dbl>    <dbl>     <dbl>
## 1 (Intercept)   3.23      1.50        2.15  0.0316    0.694    6.80  
## 2 fault_err    -0.0904    0.0432     -2.09  0.0366   -0.193   -0.0182

tidy(open_mod1, conf.int=TRUE, exp=T)

## # A tibble: 2 × 7
##   term        estimate std.error statistic p.value conf.low conf.high
##   <chr>          <dbl>     <dbl>     <dbl>   <dbl>    <dbl>     <dbl>
## 1 (Intercept)   25.3      1.50        2.15  0.0316    2.00    897.   
## 2 fault_err      0.914    0.0432     -2.09  0.0366    0.824     0.982

In this model, we can interpret ˆβ1=−0.09 and exp(ˆβ1)=exp(−0.09)=0.914 as

• A difference of 1 fault or error is associated with an estimated difference of 0.09 lower log odds (95% CI: -0.193, -0.018) of winning a tennis match at the 2013 US Open.
• A difference of 1 fault or error is associated with an estimated odds ratio of 0.914 (95% CI: 0.824, 0.982) for winning a tennis match at the 2013 US Open.

18.5 Multiple Logistic Regression

In our examples so far, we have considered only one predictor variable. Almost all practical analyses consider multiple predictor variables. This leads to multiple logistic regression.

18.5.1 Coefficient Interpretation

logit(pi)=β0+β1xi1+β2xi2+⋯+βkxik exp(cβk) is the odds ratio for a c-unit difference in variable k, when all other variables are held constant.

• In practice, the log odds do not lie on a perfectly straight line.
• We are estimating a general trend in the data

“On average, the odds of [outcome] are exp(cβk) times larger for every c-unit difference in [variable k] among observations with the same values of the other variables.”